포니아범.ai

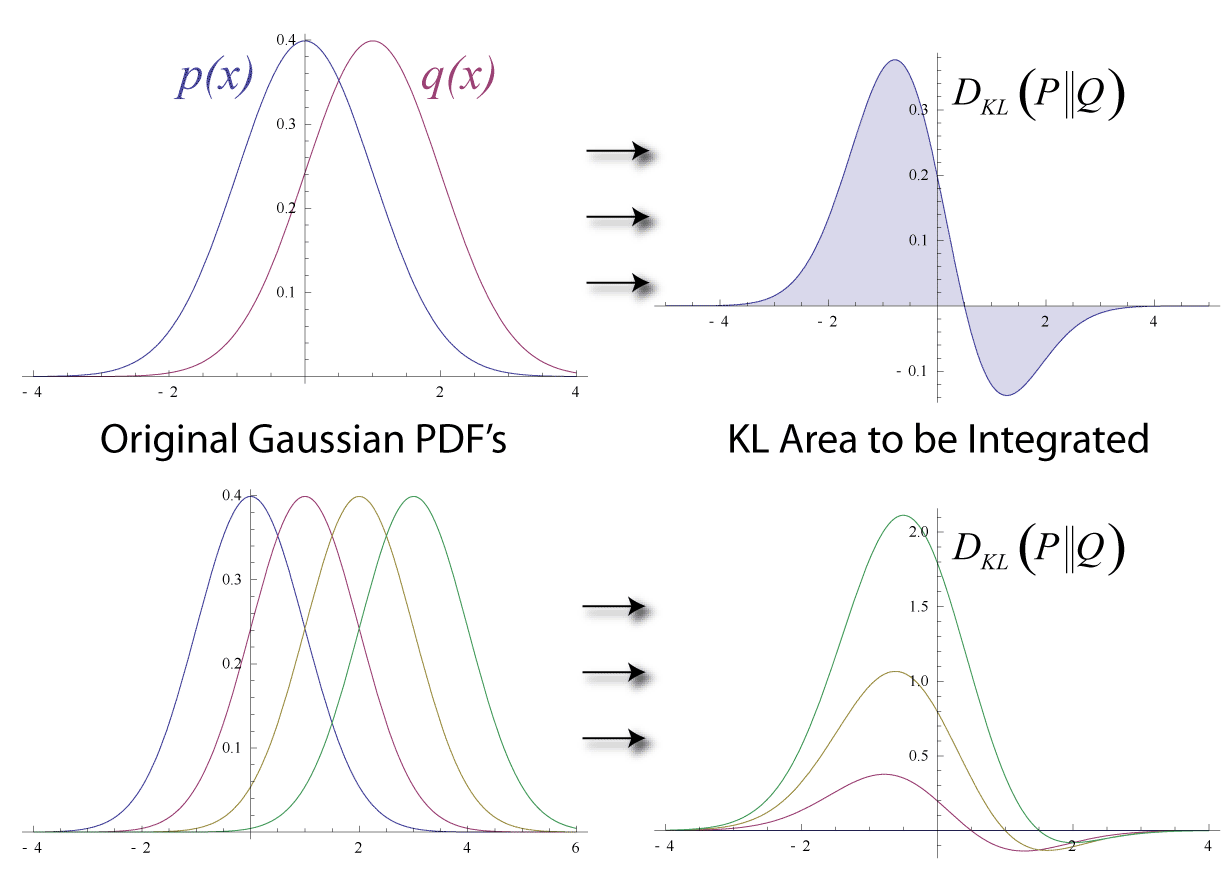
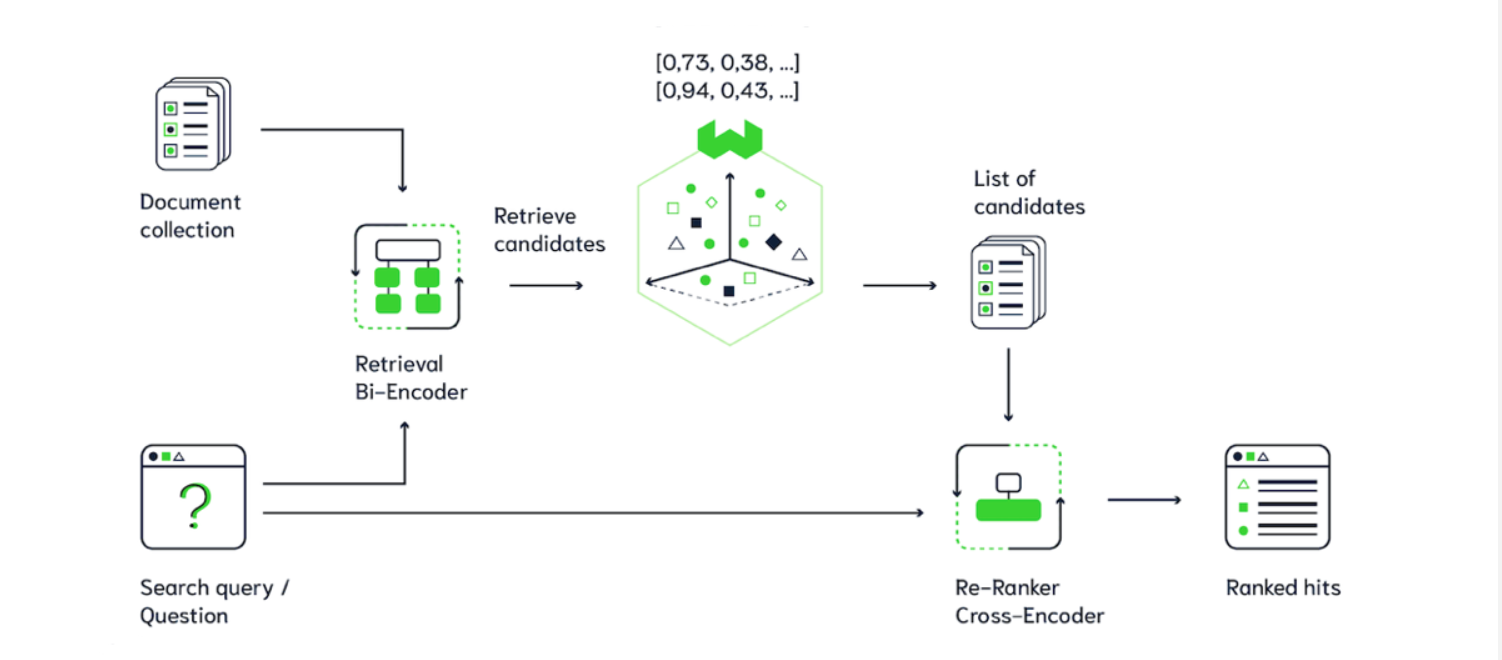
들어가며앞서 우리는 섀넌 엔트로피, 크로스 엔트로피, KL Divergence 를 통해 정보량, 불확실성, 그리고 확률 분포 간의 차이를 정량화하는 방법을 살펴보았습니다. 이제 정보 이론의 또 다른 핵심 개념인 상호 정보량 (Mutual Information, MI) 을 탐구하며, 두 확률 변수 사이의 상호 의존성 (mutual dependence) 또는 공유 정보량 (shared information) 을 측정하는 방법을 알아보겠습니다.Mutual Information 이란? - 변수 간의 관계성 측정일상 생활에서 우리는 종종 변수들 사이의 관계에 주목합니다. 예를 들어, "키가 클수록 몸무게가 많이 나갈 가능성이 높다" 거나, "날씨가 더울수록 아이스크림 판매량이 증가한다" 와 같은 경험적 관계를 인..

들어가며정보 이론과 통계학의 발전 과정에서 "두 확률 분포가 얼마나 다른가?" 라는 근본적인 질문에 대한 답을 찾기 위한 노력이 지속되었습니다. 1951년, 솔로몬 쿨백 (Solomon Kullback) 과 리처드 라이블러 (Richard Leibler)는 두 확률 분포 사이의 상대 엔트로피 (relative entropy), 즉 KL Divergence 를 제안하여 이 질문에 대한 획기적인 해답을 제시했습니다.KL Divergence 는 두 확률 분포 $P$ 와 $Q$ 의 차이를 측정하는 정보 이론적 척도입니다. $P$ 를 "기준 분포" 또는 "참 분포", $Q$ 를 "근사 분포" 또는 "모델 분포" 라고 할 때, $D_{KL}(P||Q)$ 는 $Q$ 로 $P$ 를 근사할 때 발생하는 정보량 손실, 또..

들어가며이번 포스팅에서는 이전에 알아본 섀넌 엔트로피의 수식을 살펴보고 왜 크로스엔트로피가 손실함수로서 사용되는지에 대해 살펴보겠습니다.섀넌의 엔트로피 수식 심층 분석클로드 섀넌은 1948년 논문 "통신 수학 이론 (A Mathematical Theory of Communication)"에서 정보 엔트로피 개념을 확립했습니다. 이는 불확실성을 정량화하고 정보량을 객관적으로 측정하는 혁신적인 시도였습니다. 섀넌 엔트로피는 정보 이론의 초석이자, 크로스 엔트로피를 이해하는 출발점입니다.섀넌 엔트로피 수식은 다음과 같습니다.$$H(X) = - \sum_{i=1}^{n} p(x_i) \log_2 p(x_i)$$이 수식은 확률 변수 $X$가 가질 수 있는 $n$개의 값 ($x_i$)과 그 확률 분포 $p(x_i)..

들어가며1940년대, 제2차 세계대전을 거치며 효율적이고 안전한 통신의 필요성이 그 어느 때보다 커졌습니다. 당시 과학자들은 몇 가지 근본적인 문제에 직면해 있었습니다."어떻게 하면 제한된 통신 채널로 더 많은 정보를 보낼 수 있을까?""노이즈가 있는 환경에서 어떻게 정확한 통신을 할 수 있을까?""정보의 양은 어떻게 측정할 수 있을까?"이러한 질문들에 답하기 위해서는 먼저 '정보'라는 추상적인 개념을 수학적으로 정의하고 측정할 수 있어야 했습니다. 1948년, 클로드 섀넌의 "통신의 수학적 이론"은 이 문제에 대한 혁신적인 해답을 제시했습니다.정보의 기본 단위, 비트(Bit)의 탄생벨 연구소의 젊은 연구원이었던 클로드 섀넌이 주목한 것은 인간이 주고받는 모든 메시지가 '예/아니오'의 단순한 선택들로 이..

들어가며루드비히 볼츠만(Ludwig Boltzmann, 1844-1906)은 클라우지우스의 열역학적 엔트로피 개념($dS = \frac{δQ_{rev}}{T}$)이 내포한 근본적인 질문, 즉 "엔트로피는 왜 증가하는가?"에 대한 해답을 탐구했습니다. 클라우지우스의 정의는 현상론적으로 엔트로피 증가 법칙을 기술했지만, 비가역 과정의 미시적 기원과 엔트로피 증가의 본질에 대한 심층적인 설명을 제공하지 못했습니다. 볼츠만은 이러한 한계를 극복하고 엔트로피를 미시적 관점에서 재해석하는 혁명적인 시도를 감행했습니다.볼츠만 엔트로피의 탄생 배경: 미시적 세계로의 탐구열역학적 미스터리: 비가역성과 엔트로피 증가19세기 후반, 열역학은 거시적 현상을 기술하는 강력한 이론으로 자리매김했지만, 몇 가지 근본적인 질문에 직..

들어가며머신러닝 엔지니어라면 누구나 마주하는 순간이 있습니다. 바로 모델 학습 과정에서 손실 함수로 크로스 엔트로피(Cross Entropy)를 설정하는 순간입니다. 이전에는 단순히 수식을 이해하면서 정답 데이터와 예측 데이터의 차이를 계산하는 방법이라고 이해하였는데 문득 데이터의 정보량이란 무엇이고 어떤 의미를 가지는지 등 엔트로피 자체에 대한 궁금증이 커져 갔습니다.검색을 통해 여러 자료를 공부하였고 그중 성균관대학교 뇌과학 교수님들이 운영하는 신인류라는 유튜브 채널에서 엔트로피 4부작을 보게 되었습니다. 엔트로피에 대한 전반적인 내용을 역사적으로 훑으면서 머신러닝에서 사용하는 방식까지 개괄적으로 설명해 주는 훌륭한 콘텐츠였습니다. 다만 너무 훅훅 지나가서 하나하나에 대해서 좀 더 자세하게 설명해주었..

https://transformer-circuits.pub/2021/framework/index.html A Mathematical Framework for Transformer CircuitsContents Transformer language models are an emerging technology that is gaining increasingly broad real-world use, for example in systems like GPT-3 , LaMDA , Codex , Meena , Gopher , and similar models.  However, as these models scale, their open-endednetransformer-circuits.pub이번 포스팅에서는 T..

20일에 Anthropic에서 Introducing Contextual Retriever이라는 제목으로 새로운 Article을 개제했다. (링크)기존의 RAG 방식의 문제점을 개선하기위해 나온 방법이라고해서 리뷰해보겠다. 기존의 문제점기존 RAG에서는 문서를 효율적으로 검색하기 위해 작은 chunk로 나누지만 검색된 각각의 chunk는 문맥적인 정보가 부족하다는 단점이 있다. 그래서 사람이 직접 문장을 나누거나 embedding을 통해 문장의 유사도를 계산해 문서를 나누는 semantic chunk 를 수행하기도 하고 chunk에 문서를 요약한 내용을 넣어준다거나 가상의 문서를 만들어 임베딩하고 요약한 내용만을 인덱싱하는 등 다양한 방법들이 시도 되었다. Contextual Retriever 소개이번에 ..

2024.09.22 - [RAG Project] - [RAG Project] GlobalMacro QA chatbot - Reranker&more Evaluation (9) [RAG Project] GlobalMacro QA chatbot - Reranker&more Evaluation (9)2024.09.20 - [RAG Project] - [RAG Project] GlobalMacro QA chatbot - Question Process&Evaluation (8) [RAG Project] GlobalMacro QA chatbot - Question Process&Evaluation (8)2024.09.17 - [RAG Project] - [RAG Project] GlobalMacro QA chatbo..

2024.09.20 - [RAG Project] - [RAG Project] GlobalMacro QA chatbot - Question Process&Evaluation (8) [RAG Project] GlobalMacro QA chatbot - Question Process&Evaluation (8)2024.09.17 - [RAG Project] - [RAG Project] GlobalMacro QA chatbot - Retriever&Evaluation (7) [RAG Project] GlobalMacro QA chatbot - Retriever&Evaluation (7)2024.09.12 - [RAG Project] - [RAG Project] GlobalMacro QA chatbot - Embe..